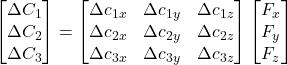Design and fabrication of a 3-dimensional capacitive-based force sensor

Motivation

Gait analysis is an important aspect of developing personalized rehabilitation techniques. To perform kinetic gait analysis, it is necessary to measure ground reaction forces (GRFs). While force plates or instrumented treadmills are commonly used in labs and clinical settings, they have limitations. For example, only a few steps can be measured on a force plate and treadmill walking does not accurately mimic overground walking. In addition, these tools cannot measure GRFs in unstructured environments, such as on uneven or uphill-downhill surfaces. To overcome these limitations, a wearable system is needed to measure GRFs for kinetic gait analysis.

Most wearable systems for measuring GRFs have one of two approaches: they either predict all three components of GRFs using kinematic gait analysis data and inverse dynamics, or they measure the vertical component using pressure sensors and estimate the other two shear components using statistical methods or kinematic data. To measure all three components of GRFs directly, a three-axis force measuring sensor that can be embedded in a shoe is necessary.

Contribution

Perform structural and electromechanical analysis in COMSOL to design the sensor according to the requirements.
Built initial prototypes using 3D printers and final prototypes using a CNC machine and machine shop tools
Prepared G-codes using Autodesk Fusion 360 for the machining using a CNC machine
Design and developed the experimental setups and perform different tests to evaluate the performance of the sensor

Theoretical Analysis

Force-capacitance relationship

We used parallel plate capacitors for this capacitive-based force sensor.
We know that the capacitance of a parallel plate capacitor,

$C = \frac{\epsilon A}{d}$

Here, C = Capacitance of the capacitor

A = Area of the parallel plate

d = distance between two parallel plates

$\epsilon = k\epsilon_0$ where, k = relative permittivity of dielectric material and $\epsilon_0 = 8.854\times10^{-12}$

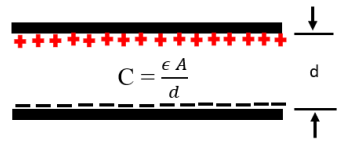
If the area of the parallel plates and the dielectric material between them is fixed, then the capacitance of the capacitor depends on the distance between the two parallel plates.

$C \propto \frac{1}{d}$

If the distance is decreased, the capacitance will increase, and if the distance is increased, the capacitance will decrease.

We can change the distance by applying force. If the capacitance change is linear in terms of applied force, F we can write -

$\Delta C = \Delta c F$

If the force has three components, for example $F_x, F_y, and F_z$ , then the total capacitance change -

$\Delta C = \Delta c_x F_x + \Delta c_y F_y + \Delta c_z F_z$

So, for above three capacitors the three capacitance change equations are -

$\Delta C_1 = \Delta c_{1x} F_x + \Delta c_{1y} F_y + \Delta c_{1z} F_z$

$\Delta C_2 = \Delta c_{2x} F_x + \Delta c_{2y} F_y + \Delta c_{2z} F_z$

$\Delta C_3 = \Delta c_{3x} F_x + \Delta c_{3y} F_y + \Delta c_{3z} F_z$

We can write above three equations in vector-matrix form -

$\begin{bmatrix}\Delta C_1\\ \Delta C_2\\ \Delta C_3\end{bmatrix} = \begin{bmatrix} \Delta c_{1x}&\Delta c_{1y}&\Delta c_{1z}\\ \Delta c_{2x}&\Delta c_{2y}&\Delta c_{2z}\\ \Delta c_{3x}&\Delta c_{3y}&\Delta c_{3z} \end{bmatrix} \begin{bmatrix} F_x \\ F_y \\ F_z \end{bmatrix}$