![]()
![]()
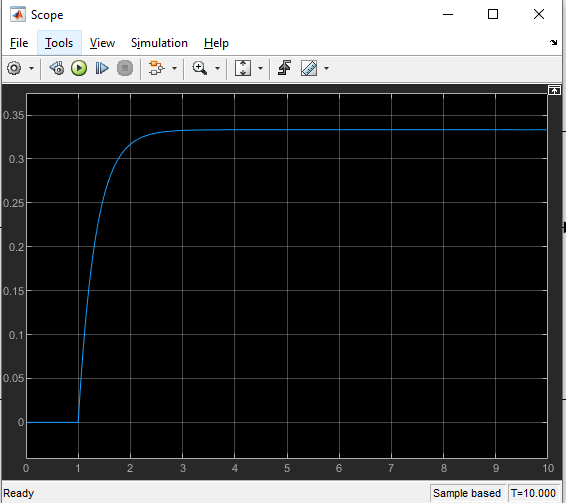
By using state_space block of the simulink, we can see the behavior of this system. Here, we will see the output of the given system for a unit-step input u (t).
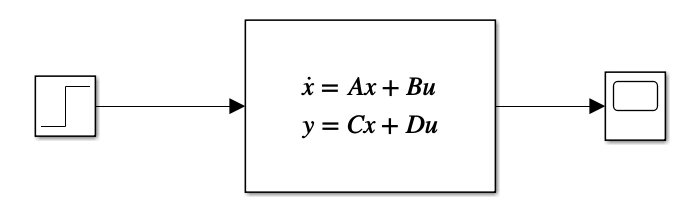
From the state space representation, in this system we have -
![]()
![]()
![]()
D = 0
Initial Condition:
![]()
So, update the state-space block according to the above -
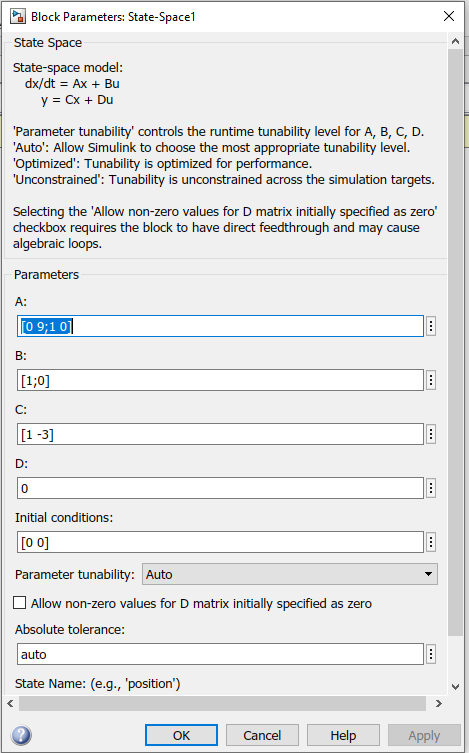
After running the simulation, from the scope, we can see the output response of the given system.
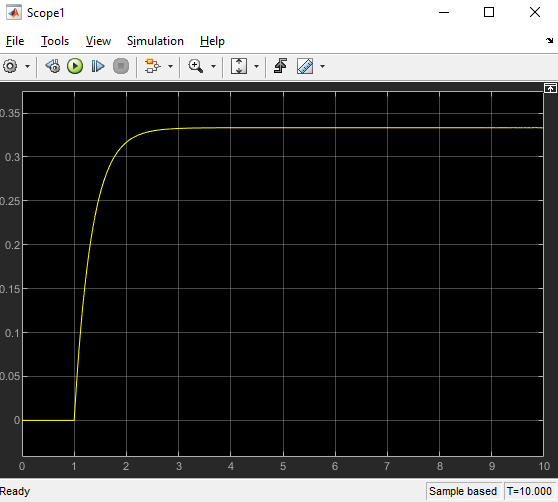
Instead of using Simulink state-space block, we can draw the system and can see the output response from the scope.
Steps:
1) From the Simulink Library Browser > Simulink > Continuous, have as many integrator (1/s) as the no. of state variables

2) Put x_dot and x before and after each integrator

4) Insert the output at the rightmost. Here, we will use a scope to see the output. From Simulink > Sinks, insert one scope block
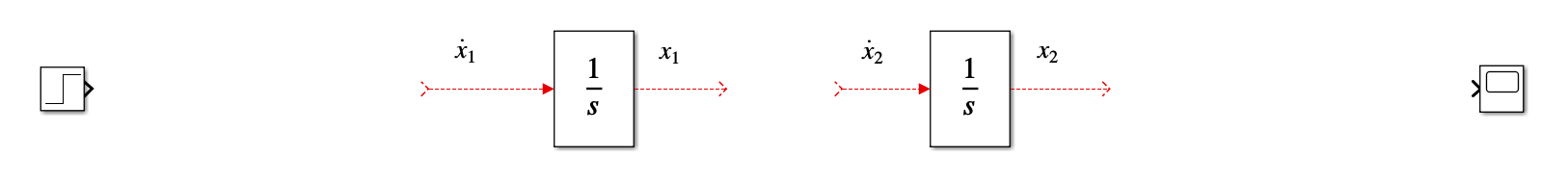
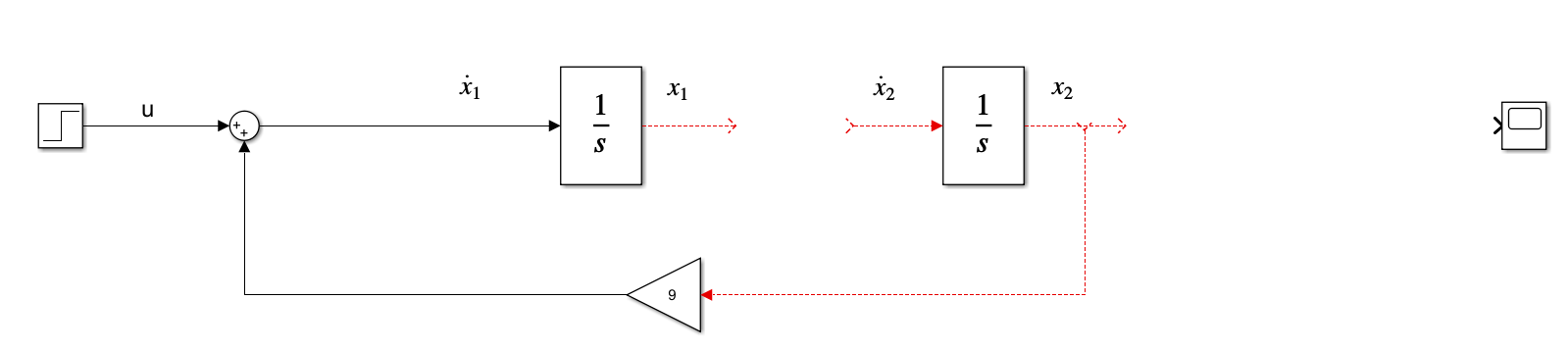
5) Write the differential equations separately, and draw them using sum and gain blocks
![]()
![]()

6) Write the output equations and draw them using sum and gain blocks
![]()
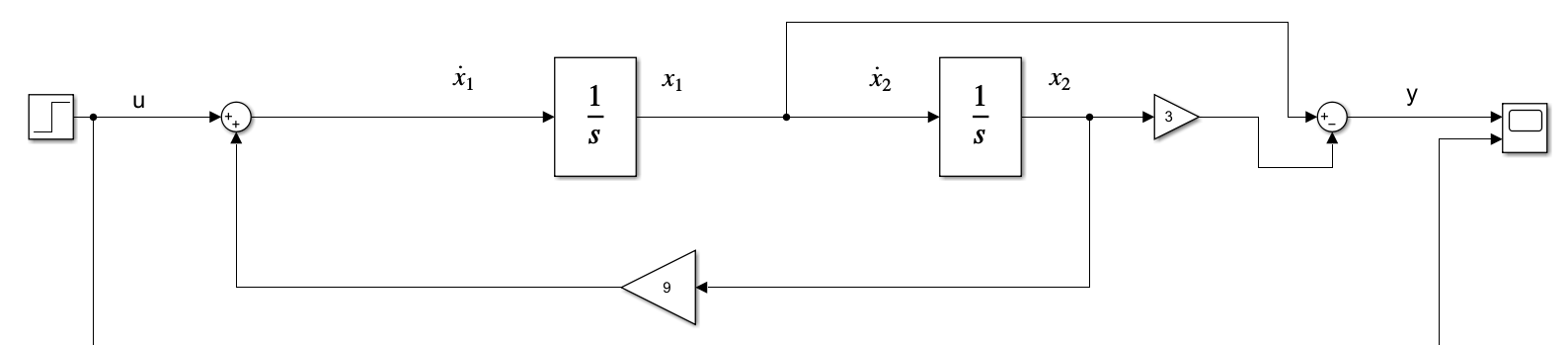
From the scope we can see that we have the same output as the previous.